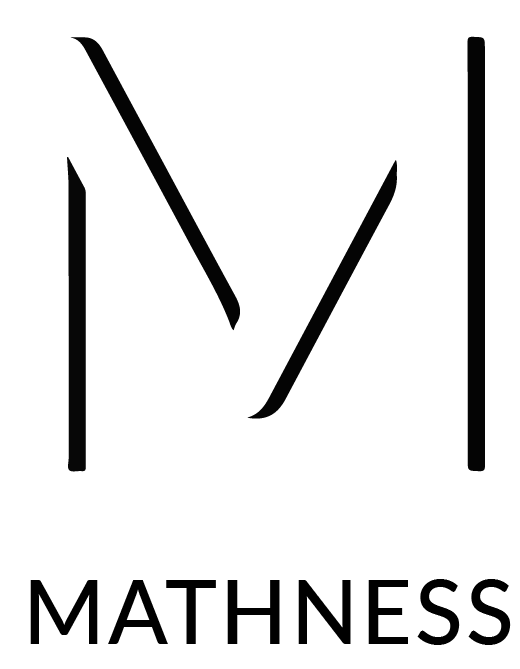Hoe maakt een zelfrijdende auto een 2D beeld van de omgeving?
In de afbeelding hieronder zie je allerlei meetapparatuur op het dak van de auto. Een deel daarvan bestaat uit 360-graden camera’s die de hele omgeving kunnen vastleggen in hoge kwaliteit. Bovendien zijn de beelden in kleur, waardoor verkeersborden correct worden afgelezen
Een zelfrijdende auto van Uber met een chauffeur achter het stuur voor eventuele ingrepen. Bron: The New York Times.
Hoe wordt er een 3D beeld gemaakt van de omgeving?
Camerabeelden hebben een groot nadeel: het is niet mogelijk om diepte te zien. Anders gezegd: de auto kan nog niet, zoals wij, kijken in 3D. Om dit probleem op te lossen zit er op het dak van de auto nog een ander systeem: Lidar.
Een 3D puntenwolk van een weg en de omgeving naast de weg. Bron: TowardsDataScience.
De Lidar-techniek zorgt ervoor dat zelfrijdende auto’s hun omgeving omzetten in een 3D puntenwolk zoals je hierboven ziet. Lidar-sensoren schieten namelijk onzichtbare laserstralen af op voorwerpen in de omgeving. De voorwerpen kaatsen de laserstralen weer terug naar de sensoren en op deze manier berekent de auto de afstand tot ieder voorwerp. In de animatie hieronder is dit proces mooi weergeven. Door Lidar wordt er dus diepte toegevoegd aan de omgeving.
Een animatie van Lidar-techniek op zelfrijdende auto’s. Bron: Waymo / The Unlockr.
Hoe worden de 2D- en 3D-beelden gecombineerd?
Het voordeel van Lidar is dus diepte en een 3D-view. Het voordeel van normale camera’s is kleur en de kwaliteit van de opname in 2D. De zelfrijdende auto wil deze twee voordelen graag combineren. Daarvoor moet het de 3D-beelden samenvoegen met de 2D-beelden. Op deze manier heeft de auto de omgeving in hoge kwaliteit tot zijn beschikking en kan het tegelijkertijd inschatten hoe ver ieder punt in de omgeving van de auto is verwijderd.
Lidar-punten bovenop de camerabeelden “geplakt”. Bron: University of Oxford.
Het combineren van camerabeelden en Lidar-punten ziet eruit zoals het plaatje hierboven. Van ieder object dat is vastgelegd op de camera bestaat ook een 3D puntenwolk verkregen door Lidar. De computer van de auto moet er nu voor zorgen dat de camerabeelden en de 3D punten correct op elkaar worden “geplakt”.
Hoe worden radialen gebruikt?
Doordat Lidar en de camera’s de hele omgeving in een 360-view observeren, wordt het samenvoegen van de beelden gedaan met behulp van een cirkel en hoeken. Aan ieder 2D punt van de camera en aan ieder 3D punt van de Lidar wordt een hoek toegewezen.
Staat er een fietser precies aan de voorkant van de auto, dan krijgen die punten een hoek van 0π radialen (0°) toegewezen. Staat de fietser precies aan de achterkant, dan krijgen de punten een hoek van π radialen (180°) toegewezen.
De hoeken kun je dus zien als een label. Ieder punt heeft nu een hoek-label en door de labels te matchen kun je nu de 2D camerabeelden combineren met de 3D Lidar-punten.
Waarom radialen en geen graden?
Over het algemeen worden hoeken uitgedrukt in graden. In de wetenschap en in de techniek wordt er meer gebruik gemaakt van radialen als eenheid voor hoeken. Eén van de redenen hiervoor is dat het wat makkelijker rekent.
Ten eerste kun je je afvragen waarom een rechte hoek 90° is. Waarom geen 91° of 100°? Ten tweede leidt het gebruik van graden soms tot onhandige situaties. Bijvoorbeeld bij het tekenen van de sinusfunctie. De standaard sinusfunctie beweegt verticaal tussen -1 en 1. Op de y-as heb je daarom maar twee hokjes nodig op ruitjespapier. Werk je met graden op de x-as? Dan heb je maar liefst 360 hokjes nodig om de sinusfunctie netjes op dezelfde schaal te tekenen! Bij radialen zijn hoeken en afstanden aan elkaar gerelateerd waardoor ze beter tot elkaar in verhouding staan. Dat wordt hieronder verder uitgelegd.
Wat is een radiaal eigenlijk?
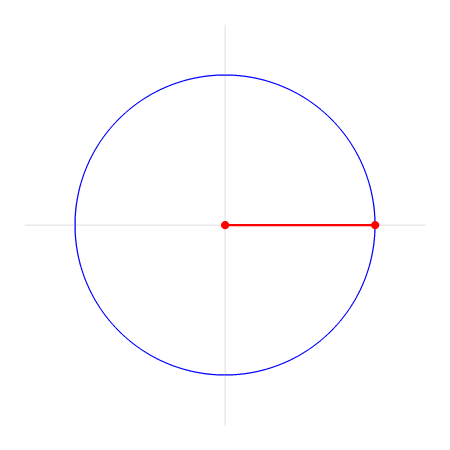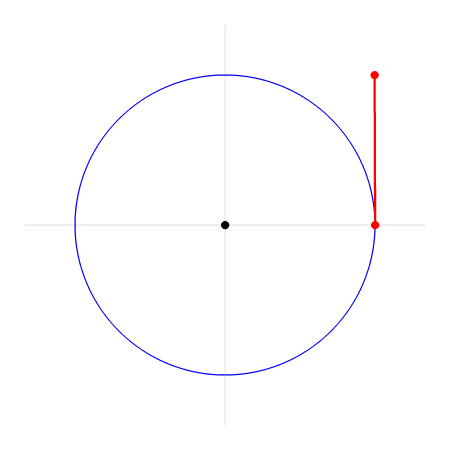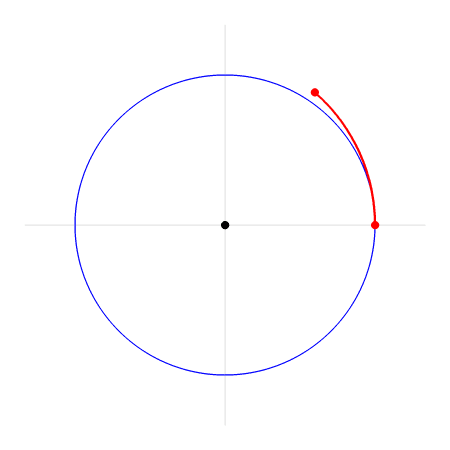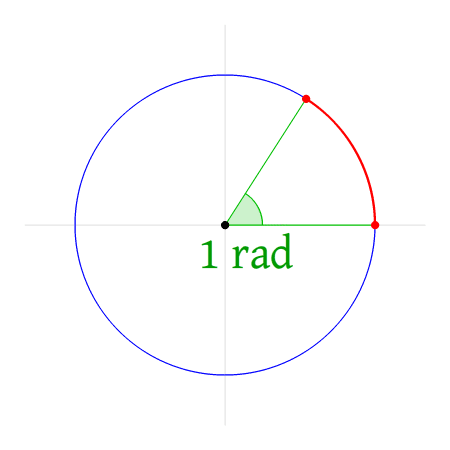
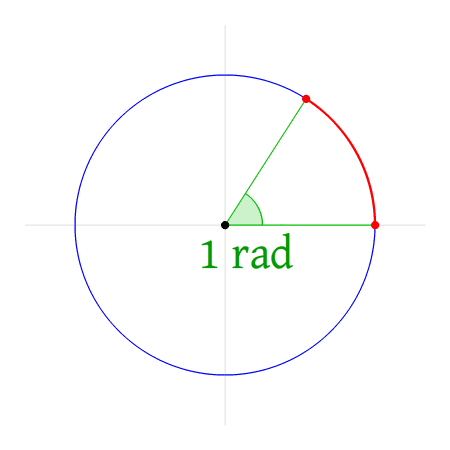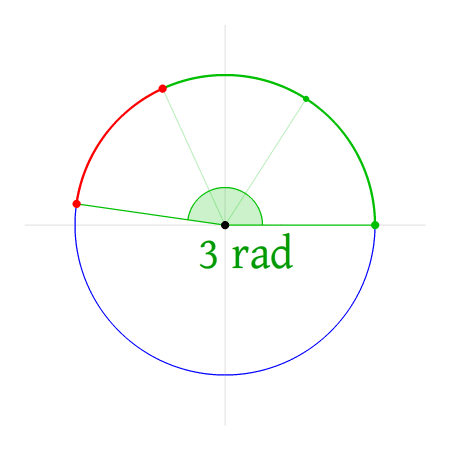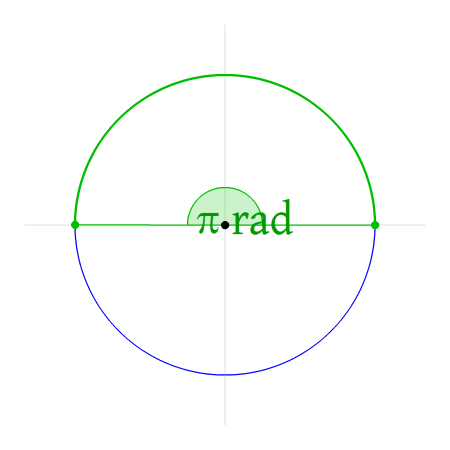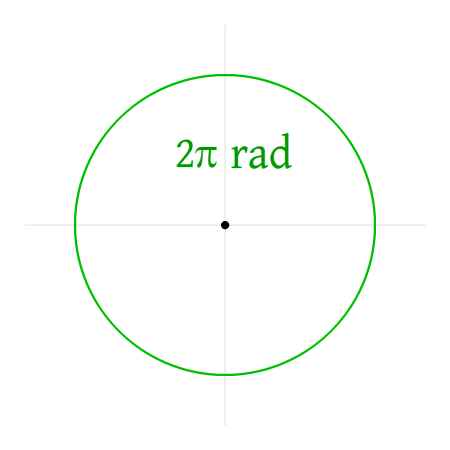
Radialen zijn gedefinieerd op een cirkel. In dit voorbeeld kijken we naar de eenheidscirkel: een cirkel met straal 1. In de animatie hieronder zie je wat 1 rad (radiaal) betekent.
Animatie: Lucas Vieira.
Het rode lijntje is de straal en heeft dus lengte 1. De hoek 1 rad (radiaal) is de hoek die je krijgt als je op de eenheidscirkel de afstand van eenmaal de straal aflegt.
Een hoek van 3 radialen is dan de hoek die je krijgt als je driemaal de afstand van de straal op de cirkel hebt doorlopen. Werk je met radialen? Dan kom je ongetwijfeld de constante π (3.14…) tegen. Een hoek van π radialen is de hoek die je krijgt als je 3.14… maal de afstand van de straal op de cirkel hebt doorlopen. Deze afstand is precies de afstand van de halve cirkel omdat de omtrek van de cirkel met straal 1 gelijk is aan 2π.
Animatie: Lucas Vieira.
Een hoek van 2π radialen komt overeen met een heel rondje over de cirkel lopen. Of anders gezegd: een afstand afleggen van 2π maal de straal van de cirkel. Bij het gebruik van radialen zijn dus de hoeken en de afstanden direct aan elkaar gerelateerd.
Voor meer informatie en oefeningen met radialen, klik hier.