Wat is een geluidsgolf?
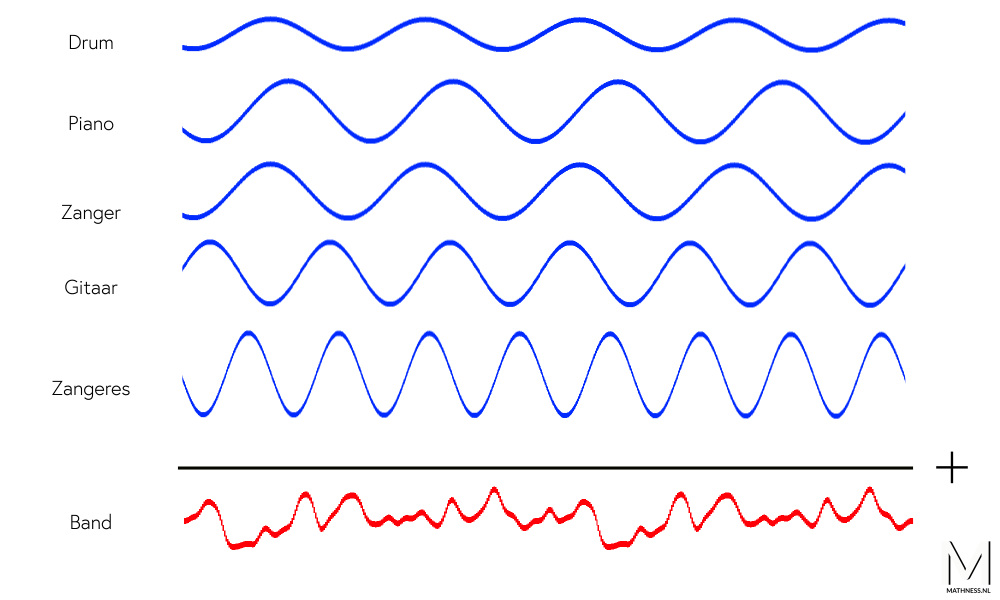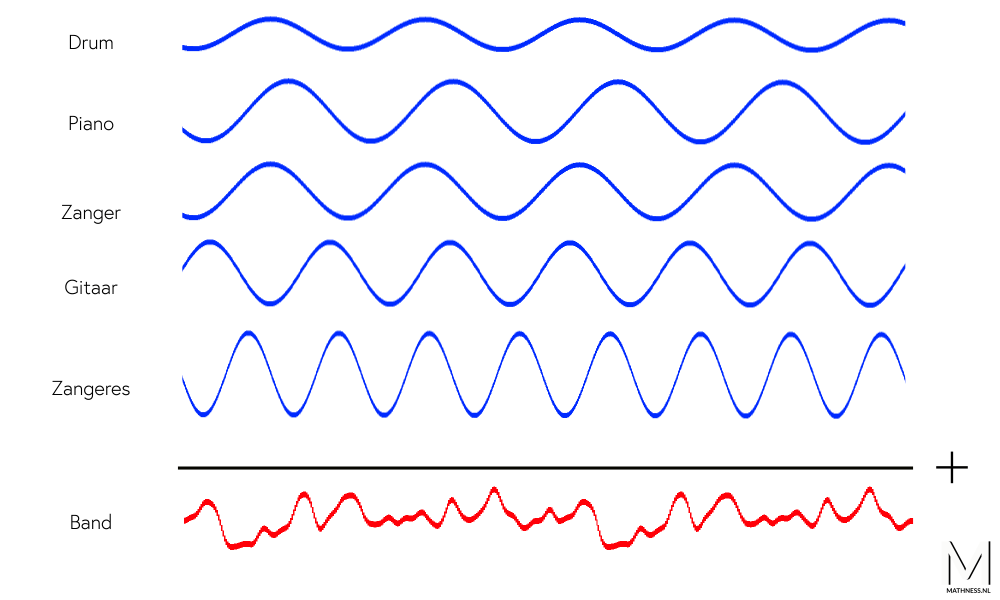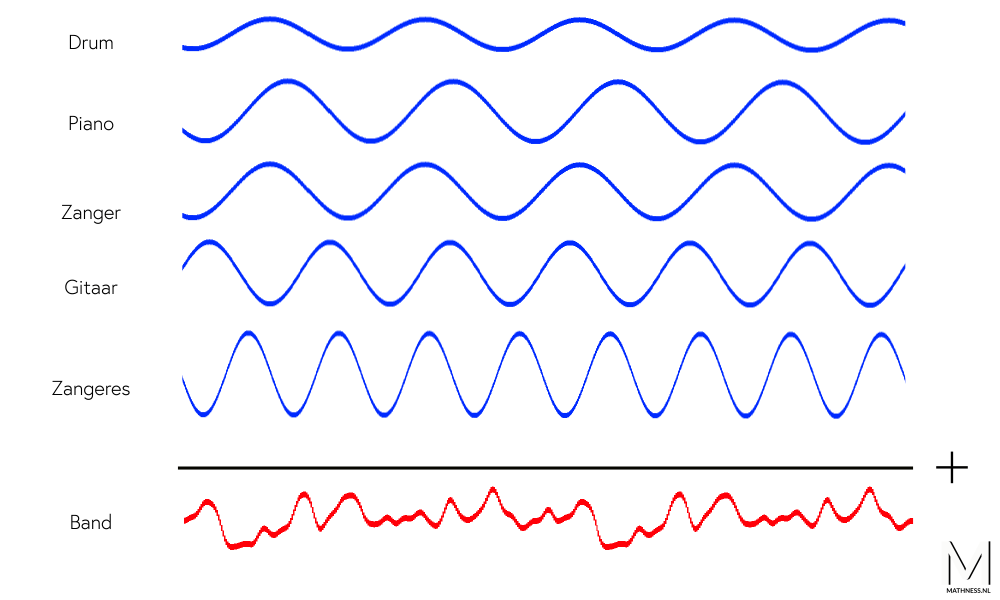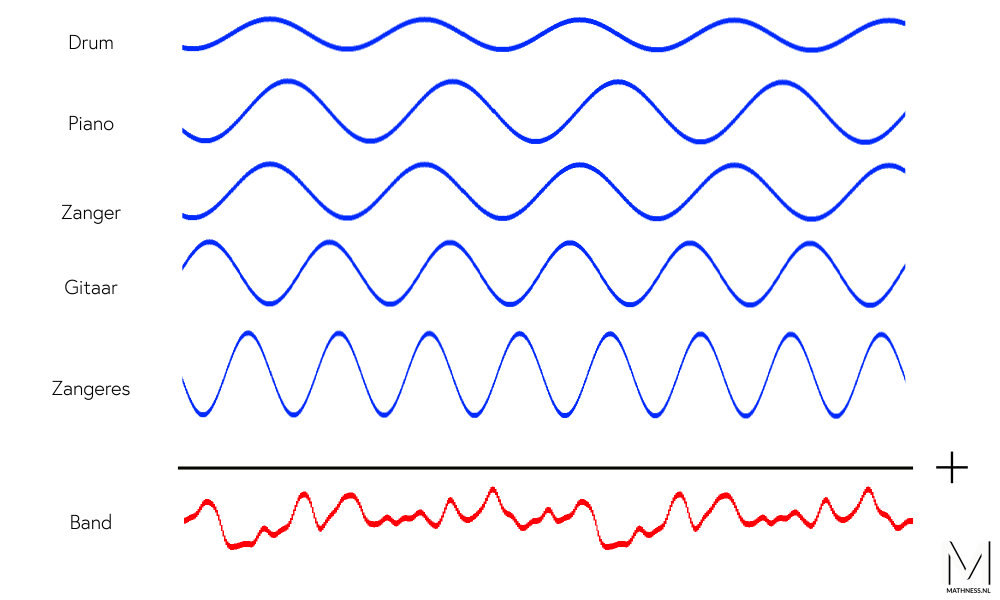
Geluid, of het nou muziek is of je eigen stem, verplaatst zich als een onzichtbare golf. Het geluid dat je hoort als je een gitaarsnaar aanslaat ziet eruit zoals de animatie hieronder.
Sla je een andere snaar aan, dan hoor je een andere toon en de golf die daarbij hoort heeft een andere vorm. Ieder geluid heeft dus zijn eigen type geluidsgolf. Daarom produceert iedere zanger, zangeres of muzikant zijn of haar eigen geluidsgolven.
De geluidsgolven zijn versimpeld voor deze animatie.
De blauwe golven hierboven staan voor het geluid van alle individuele leden van de band. Tel je al deze golven bij elkaar op, dan krijg je de rode samengestelde golf: de geluidsgolf van de hele band. De rode golf is dus wat je hoort als je naar een band of een nummer luistert.
Hoe bedenkt je telefoon welk nummer bij een geluidsgolf hoort?
Elk nummer heeft een unieke geluidsgolf. Deze geluidsgolf wordt gezien als de digitale vingerafdruk van een nummer.
De digitale vingerafdruk wordt door je telefoon vervolgens vergeleken met de digitale vingerafdrukken van alle nummers. Wordt er een match gevonden? Dan verschijnt de titel en artiest op je beeldscherm!
De geluidsgolf van een nummer kan er nogal complex uitzien. Het is daarom lastig om in één keer te zien wat het bijbehorende nummer is. Je telefoon zoekt daarom eerst uit waar deze golf uit is opgebouwd. De golf van de hele band wordt dus ontleed in verschillende golven van de bandleden, dat is hieronder in de animatie goed te zien:
Een nieuw voorbeeld van een samengestelde (rode) golf. De rode golf wordt ontleed in kleinere blauwe golfjes. Animatie: Lucas V. Barbosa.
De blauwe golfjes van hierboven kun je zien als de bouwstenen van de rode golf en vormen samen dus precies de rode golf. Iedere rode golf heeft een unieke samenstelling van blauwe golfjes. Je kan daarom een nummer herkennen aan deze samenstelling van blauwe golfjes. De blauwe golfjes vormen met elkaar de digitale vingerafdruk van het nummer.
Waarvoor worden de sinusoïden gebruikt?
Om de digitale vingerafdruk samen te stellen moet je telefoon kunnen kiezen uit een grote verzameling van verschillende geluidsgolven. Deze golven zijn de sinusoïden
De meest eenvoudige sinusoïde krijg je met de parameters: a=0, b=1, c=1, d=0:
Door verschillende waarden voor parameters a,b,c en d te nemen kan je een verzameling maken met veel verschillende soorten blauwe golfjes. Hieronder zie je bijvoorbeeld vier verschillende sinusoïden die horen bij verschillende waarden voor parameter c.
Je kan hier goed zien dat verschillende waarden van c, verschillende periodes oplevert. Bij natuurkunde heb je het dan over de golflengte van de geluidsgolf. Bij een lage stem hoort bijvoorbeeld een langere periode dan bij een hoge stem.
Verschillende waarden van parameter b geeft verschillende hoogtes van de golf aan. Dit is de amplitude en hiermee kan je golfjes schalen. Een grote golf (hoge amplitude) hoort bijvoorbeeld bij een hard geluid.
Hoe wordt de digitale vingerafdruk gemaakt?
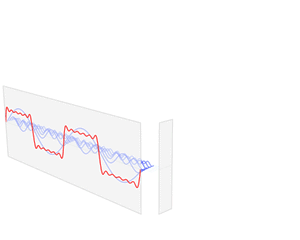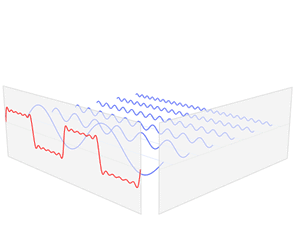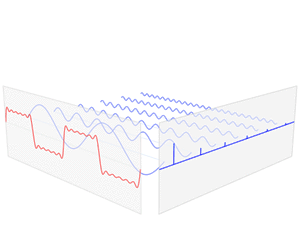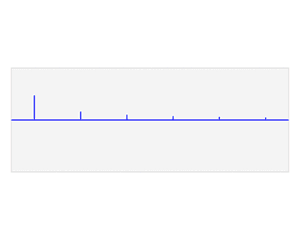
Met de sinusoïden kan je telefoon dus een grote verzameling van verschillende soorten geluidsgolven maken. Met behulp van een wiskundige techniek (Fourier Transformaties) kiest je telefoon precies de juiste golven uit waaruit de geluidsgolf van het hele nummer is opgebouwd. Deze informatie wordt onthouden in de balk met verticale streepjes in onderstaande animatie:
Animatie: Lucas V. Barbosa.
De plek van de streepjes op de blauwe balk geeft aan met welke golf je te maken hebt (periode). De hoogte van het streepje geeft aan in welke mate het golfje wordt vergroot (amplitude). Je ziet bijvoorbeeld dat het eerste blauwe golfje het meeste is vergroot. Deze golf heeft dus de grootste amplitude en daarom is het eerste streepje in de balk het hoogste.
Bron: Lucas V. Barbosa.
Dit blauwe balkje vertelt het algoritme dus hoe de rode golf moet worden nagemaakt. De rode golf van hierboven zou je kunnen zien als een klein stukje van het nummer, bijvoorbeeld een seconde van het nummer. Voor elke seconde wordt er opnieuw een blauw balkje met amplitude-streepjes gemaakt zodat het hele nummer in kaart wordt gebracht. Plak je al die balkjes achter elkaar, dan krijg je een soort digitaal berglandschap te zien zoals hieronder is weergeven.
Een voorbeeld van een digitaal berglandschap, ook wel spectrogram genoemd. Bron: Debianux.
Dit is de digitale vingerafdruk uit het verhaal en wordt ook wel spectogram genoemd. Een spectrogram heeft zoals je ziet drie dimensies (drie assen): een tijd-as, een amplitude-as en een frequentie-as. Het is gebruikelijk om frequentie te gebruiken in plaats van de periode in dit soort toepassingen.Vanuit de wis-en natuurkundelessen weet je dat de frequentie gelijk is aan: