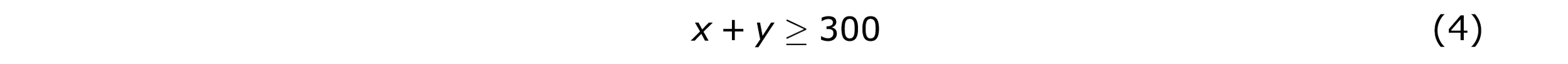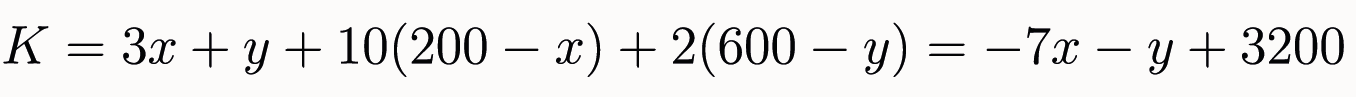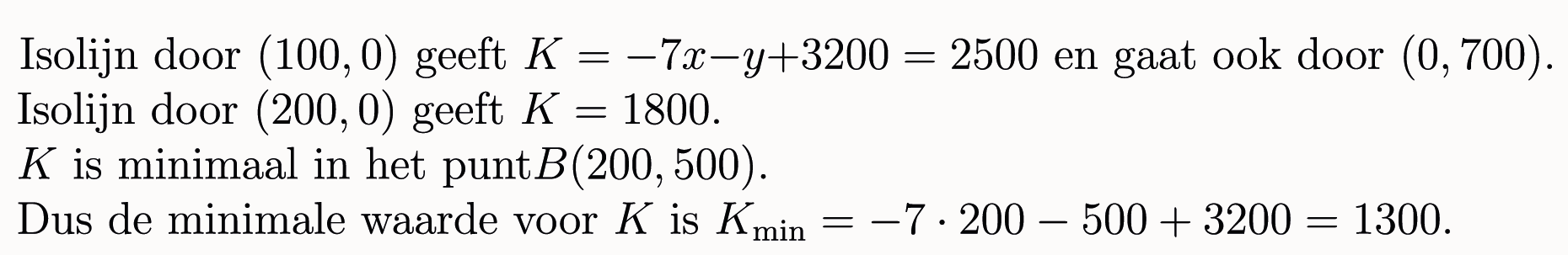Hoe wordt de voorraad geregeld in de supermarkt?
Iedere supermarkt heeft een manager die verantwoordelijk is voor de voorraad in de winkel. De manager geeft de bestellingen door aan het hoofdkantoor. Als de manager zijn werk goed doet, komt er precies op tijd een nieuwe lading binnen op het moment dat de schappen leeg dreigen te raken. Het hoofdkantoor speelt hier ook een belangrijke rol in. Zij krijgen dagelijks bestellingen van alle supermarkten in Nederland binnen. Overal op tijd de juiste voorraad leveren in heel Nederland is een probleem waar veel wiskunde voor wordt gebruikt!
Hoe krijg je op tijd de juiste voorraad binnen met zo min mogelijk kosten?
Dat is het probleem waar het hoofdkantoor zich mee bezig houdt. En dat is vrij ingewikkeld. In de eerste plaats omdat er heel veel supermarkten zijn, maar ook omdat er allerlei voorwaarden zijn waar aan gedacht moet worden.
Dagelijks rijden er honderden volle vrachtwagens van magazijnen naar supermarkten. Bij het plannen van de routes van deze vrachtwagens moet er rekening gehouden worden met belangrijke voorwaarden. Stel dat supermarkt A en B allebei hun voorraad tussen 6 en 7 uur willen ontvangen, terwijl de reistijd tussen de supermarkten langer is dan een uur. De voorraad kan dan niet in één vrachtwagen worden gestopt. Naast de reistijd en levertijd zijn er nog veel meer voorwaarden waaraan gedacht moet worden. Hoeveel producten passen in één vrachtwagen? Hoeveel vrachtwagens zijn beschikbaar? Heeft de vrachtwagen een koelsysteem?
Er wordt gezocht naar de goedkoopste route die aan dit soort voorwaarden voldoet. Er zijn bedrijven die speciaal voor hun klanten, zoals supermarkten, berekenen wat deze route is. Over het werk van dit soort bedrijven kun je lezen in het verhaal van Laura.
Een voorbeeld
Stel dat er twee magazijnen zijn met een voorraad broden. Magazijn A heeft 700 broden en Magazijn B heeft 500 broden. Er zijn ook twee supermarkten die broden hebben besteld. Supermarkt A heeft 200 broden besteld en Supermarkt B heeft 600 broden besteld. Het leveren van de broden is natuurlijk niet gratis. Daarom zijn er kosten om van een magazijn naar een supermarkt te gaan. Deze kosten kunnen verschillen. Als het magazijn dichterbij is, is het transport bijvoorbeeld goedkoper. In de figuur hieronder kun je zien dat het 3 cent kost om één brood van Magazijn A naar Supermarkt A te vervoeren.
Misschien heb je zelf al een oplossing voor het probleem bedacht. Vanuit Magazijn A kun je bijvoorbeeld 600 broden naar Supermarkt B vervoeren en 100 broden naar Supermarkt A. De overige 100 broden voor Supermarkt A komen dan van Magazijn B. In dit geval heb je een oplossing voor het probleem gevonden: alle supermarkten hebben hun broden binnen. Maar is dit ook de goedkoopste oplossing?
Hoe wordt de optimale route berekend?
Bij dit soort problemen zijn er veel verschillende manieren om het probleem op te lossen. De supermarkt is natuurlijk geïnteresseerd in de oplossing met de laagst mogelijke kosten. Maar hoe vind je deze oplossing? Met lineair programmeren!
Om te berekenen hoeveel stokbroden er vanuit elk magazijn moeten worden vervoerd, gebruiken we de variabelen x en y.
Voor de oplossing die we hierboven hebben bedacht krijgen we dan x = 100 en y = 600.
Er zijn ook bepaalde voorwaarden waar rekening mee moet worden gehouden. Magazijn A heeft 700 broden op voorraad, waardoor er vanuit Magazijn A niet meer dan 700 broden kunnen worden vervoerd. Die voorwaarden kunnen worden geschreven als vier lineaire ongelijkheden (opdracht 1).
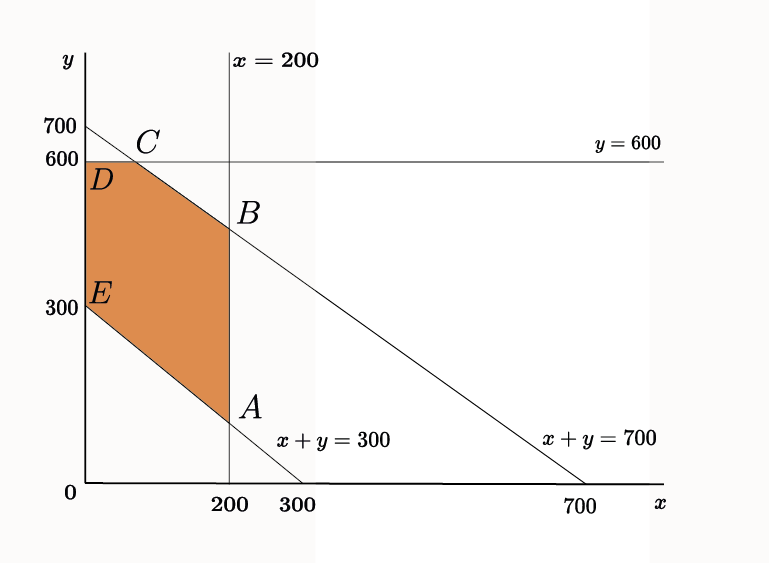
De ongelijkheden zorgen samen voor een gebied in het x,y-assenstelsel. In de figuur hieronder is dit gebied aangegeven in het oranje. Dit gebied kun je vinden met de theorie van begrensde gebieden (opdracht 2).
Elk coördinaat in het begrensde gebied is een oplossing van het probleem. In het plaatje hierboven is het coördinaat (x,y) = (100,400) als voorbeeld getekend. Dit is één van de vele oplossingen in het gebied. Maar hoe weet je nu bij welke oplossing de kosten zo laag mogelijk zijn?
Om daar een antwoord op te geven moet voor elke oplossing (x,y) precies de kosten kunnen worden berekend. De kosten K (in eurocent) kunnen we berekenen met de volgende formule (opdracht 3):
Het berekenen bij welke oplossing de kosten zo laag mogelijk zijn kun je bijvoorbeeld doen met behulp van isolijnen of de hoekpunt methode. Dit geeft de oplossing x = 200 en y = 500 met de minimale kosten K = 1300 (opdracht 4). De oplossing met de minimale kosten is dus:
De oplossing van x = 200 en y = 500 met kosten K = 1300 zorgt er dus voor dat beide supermarkten hun voorraad keurig op orde hebben tegen de laagst mogelijke kosten.
Opdracht 1
Stel dat er twee magazijnen zijn met een voorraad broden. Magazijn A heeft 700 broden en Magazijn B heeft 500 broden. Er zijn ook twee supermarkten die broden hebben besteld. Supermarkt A heeft 200 broden besteld en Supermarkt B heeft 600 broden besteld. Stel dat x en y de volgende variabelen zijn
Toon aan dat de voorwaarden geschreven kunnen worden als vier lineaire ongelijkheden:
Als x het aantal broden is dat van Magazijn A naar Supermarkt A wordt vervoerd, dan moeten er vanaf Magazijn B nog 200-x (de rest) broden naar Supermarkt A worden vervoerd. Op dezelfde manier moeten er 600-y broden worden vervoerd van Magazijn B naar Supermarkt B. Zie de figuur hieronder.
De eerste voorwaarde is logisch: je kan niet minder dan nul stokbroden vervoeren. Het aantal stokbroden dat wordt vervoerd moet daarom groter of gelijk zijn aan nul. Hierdoor krijg je de volgende voorwaarden:
Deze vier ongelijkheden samen kun je schrijven als
We weten ook dat de totale hoeveelheid broden dat wordt geleverd vanuit Magazijn A niet groter kan zijn dan 700. Dat levert de derde voorwaarde op:
De totale hoeveelheid stokbroden vanaf Magazijn B mag niet groter dan 500 stokbroden zijn. Daarom geldt:
Deze ongelijkheid kan je omschrijven tot
Opdracht 2
Teken het begrensde gebied dat hoort bij de vier lineaire ongelijkheden
Opdracht 3
Stel dat x en y de volgende variabelen zijn
In de figuur hieronder staan de kosten om een brood te vervoeren van een magazijn naar een supermarkt.
Toon aan dat de formule van de totale kosten K (in eurocent) juist is.
We weten de kosten om een brood te vervoeren van een magazijn naar een supermarkt. Als er x stokbroden worden vervoerd van Magazijn A naar Supermarkt A en het kost 3 cent per stokbrood, dan zijn de kosten 3x. Zo komen we op de formule van de totale kosten K (in eurocent):
Opdracht 4
Hoeveel broden moeten er vervoerd worden vanuit Magazijn A en Magazijn B, zodat er zo min mogelijk kosten zijn?
Minimaliseer hiervoor de kostenformule op het begrensde gebied. Je kunt hierbij de hoekpuntmethode of isolijnen gebruiken.
Hoekpuntmethode
De kostenformule neemt het minimum aan in een hoekpunt van het begrensde gebied. We berekenen daarom op elk hoekpunt wat de kosten zijn.
De minimale kosten zijn dus 13 euro. Hierbij hoort de oplossing x = 200 en y = 500. Dus vervoer 200 broden van Magazijn A naar Supermarkt A en 500 broden van Magazijn A naar Supermarkt B. Daarnaast moeten er nog 100 broden van Magazijn B naar Supermarkt B.
Isolijnen