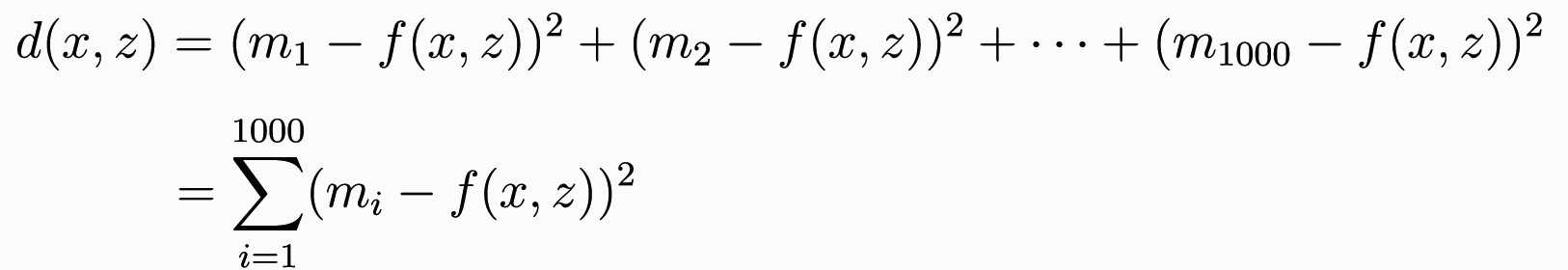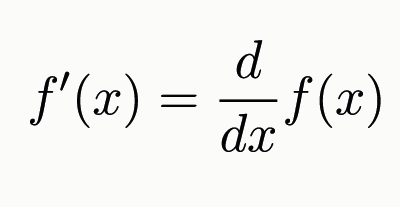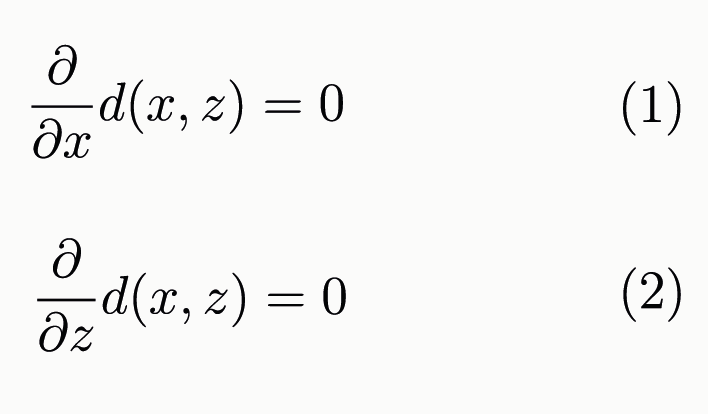Verdieping buitenaards leven & De afgeleide functie

Meerdere variabelen & Partiële afgeleides

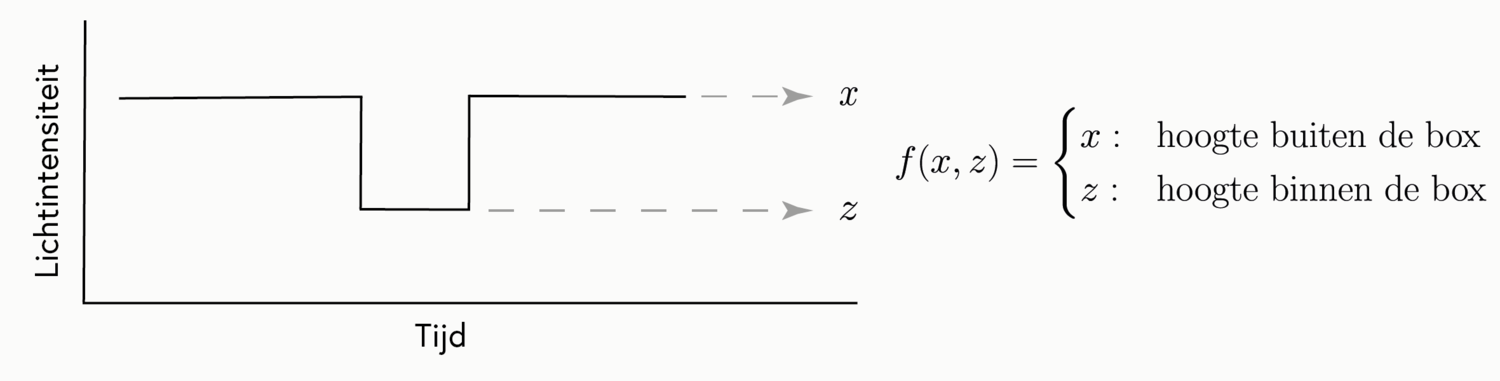
Hoe ziet de box-functie er wiskundig uit? Hieronder wordt de box-functie gedefinieerd.

Zoals je ziet is deze functie iets moeilijker dan de functies die je normaal gesproken in je boek ziet. De functie hangt namelijk af van twee variabelen: x en z. De hoogste waarde buiten de box wordt aangegeven met variabele x en de laagste waarde binnen de box met variabele z. In werkelijkheid zijn er nog meer variabelen waar rekening mee gehouden moet worden (de plaats en lengte van de box bijvoorbeeld) maar voor nu houden we het bij deze twee.

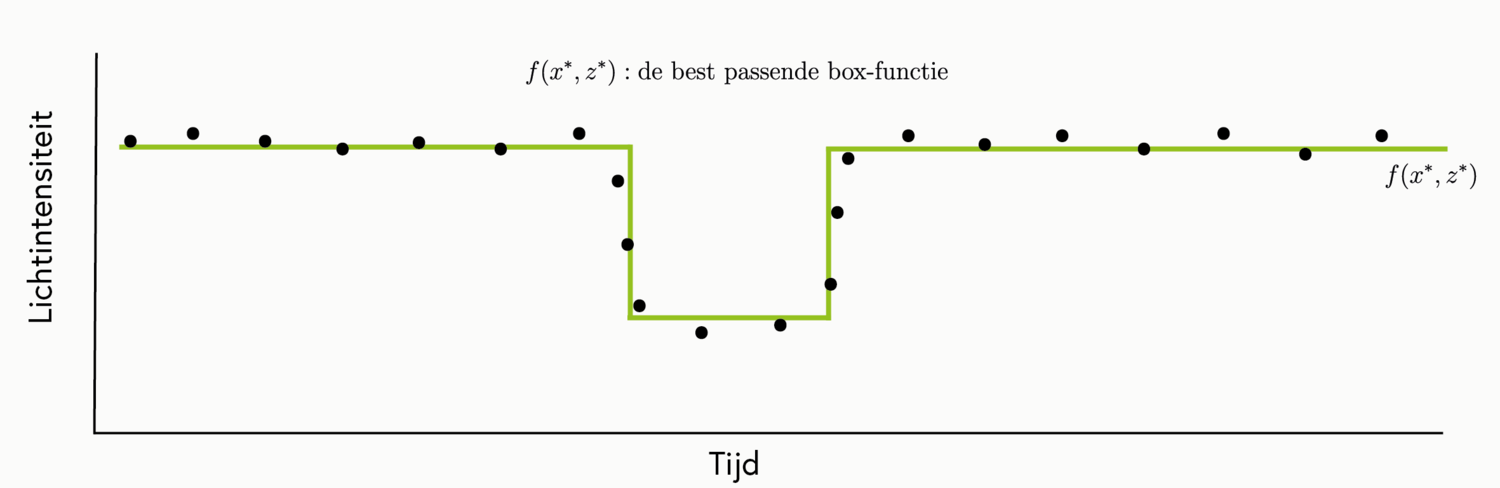
Het doel is uiteindelijk om de waarden x* en z* te berekenen die horen bij de best passende box-functie. Dit gaat op dezelfde manier als in het artikel. We stellen een afstandsfunctie op en we minimaliseren deze afstandsfunctie met behulp van de afgeleide functie. We zullen zien dat het afleiden van de functie nu anders gaat, omdat de functie nu afhankelijk is van twee variabelen.

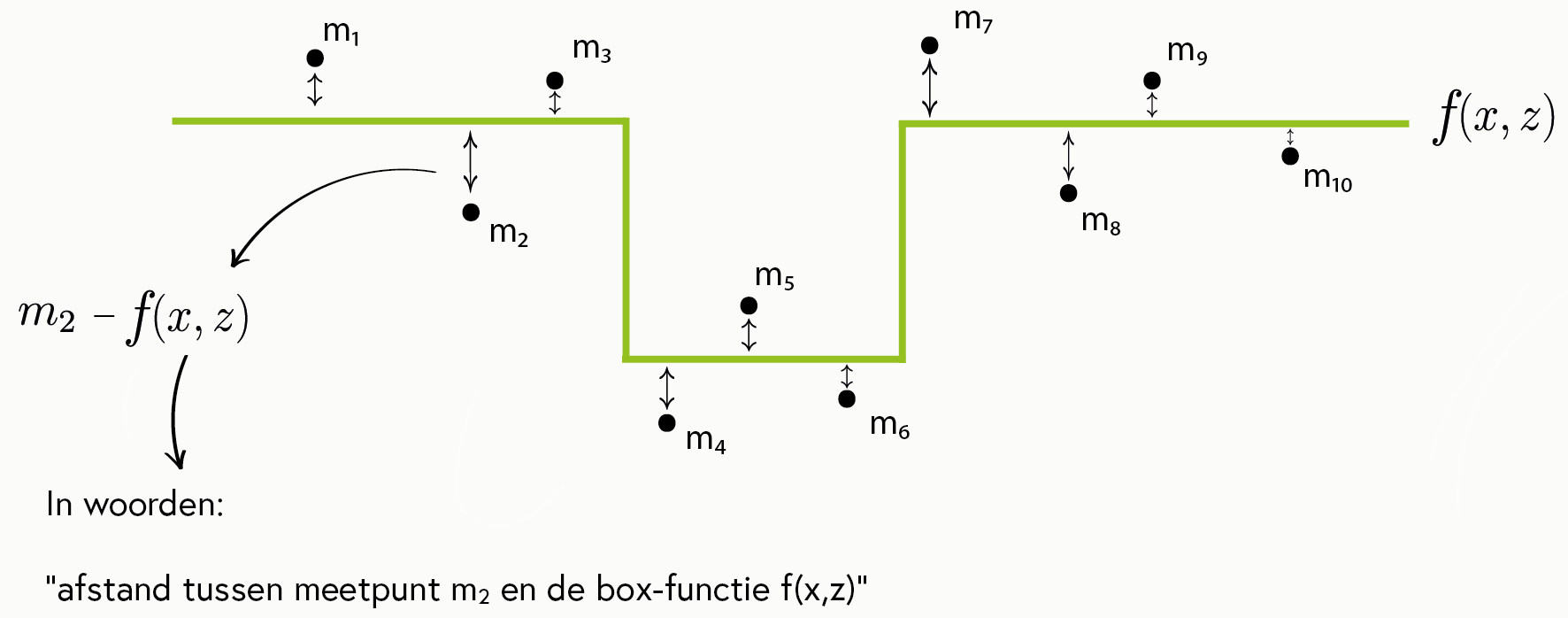
De afstandsfunctie wordt verkregen door alle afstanden tussen de meetpunten en de box-functie bij elkaar op te tellen. Met andere woorden: alle lengtes van de pijltjes worden bij elkaar opgeteld. Op deze manier ontstaat de afstandsfunctie d(x,z):

Afgeleide functie gelijkstellen aan nul

Nu er een afstandsfunctie is opgesteld kan er worden bepaald welke box-functie het beste bij het dipje in de grafiek past. Dit is namelijk de box-functie met de kleinste afstand tot de meetpunten. Hierboven heb je gelezen dat de box-functie bestaat uit een hoogste waarde x en een laagste waarde z. De box-functie met de kleinste afstand is dus de box-functie die bestaat uit de waarden voor variabelen x en z die horen bij het minimum van de afstandsfunctie d(x,z). De afstandsfunctie moet dus worden geminimaliseerd en dat doen we door de afgeleide gelijk te stellen aan nul.

De afgeleide van de afstandsfunctie d(x,z) ziet er iets anders uit dan de afgeleide functies uit je boek. Op de middelbare school hebben functies altijd één variabele, meestal de variabele x. De afgeleide functie ziet er meestal zo uit:

Meestal gebruik je de notatie f’(x). De andere notatie wordt niet veel gebruikt op de middelbare school. De dx in de noemer geeft aan naar welke variabele in de functie wordt afgeleid. In het geval van de afstandsfunctie d(x,z) is deze notatie handig omdat de afstandsfunctie afhankelijk is van twee variabelen. Als je een technische studie gaat doen zal je zien dat functies vaak meerdere variabelen hebben. Als je zo’n functie wilt afleiden spreek je van een partiële afgeleide. Dit werkt hetzelfde als op de middelbare school. De notatie is alleen anders en je moet voor elke variabele apart (partieel) de afgeleide berekenen en vervolgens gelijkstellen aan nul. Dit noteer je zo:

Het oplossen van vergelijking (1) en (2) levert waarden op voor x en z die horen bij de best passende box-functie: x* en z*.

Wat de precieze waarden van x* en z* zijn en hoe we daaraan komen, laten we voor nu even weg. Dat doen we omdat de afstandsfunctie d(x,z) een ingewikkelde functie van twee variabelen is. Het is inzichtelijker om dit proces van partiële afgeleiden te bekijken voor een “makkelijker” voorbeeld. Zie de opdracht hieronder.